Measurement of the extragalactic background light spectral energy distribution with VERITAS

 

 

Measured 68% containment on the EBL intensity as a function of wavelength, compared to recent gamma-ray measurements. For details, see Figure 6 below.

Reference: A.U. Abeysekara et al. (The VERITAS Collaboration), Astrophysical Journal 885: 150, 2019

Full text version

ArXiv: ArXiV:1910.00451

Contacts: Elisa Pueschel

Diffuse photon fields encode information about energy release over the Universe's evolution. The extragalactic background light (EBL), which spans the optical and infrared range, is dominated in the optical range by stellar emission, and in the infrared range by re-radiation of starlight after absorption by dust. It also includes contributions from energy release during galaxy formation and accretion onto active galactic nuclei. While challenging to measure directly, it can be studied through the measurements
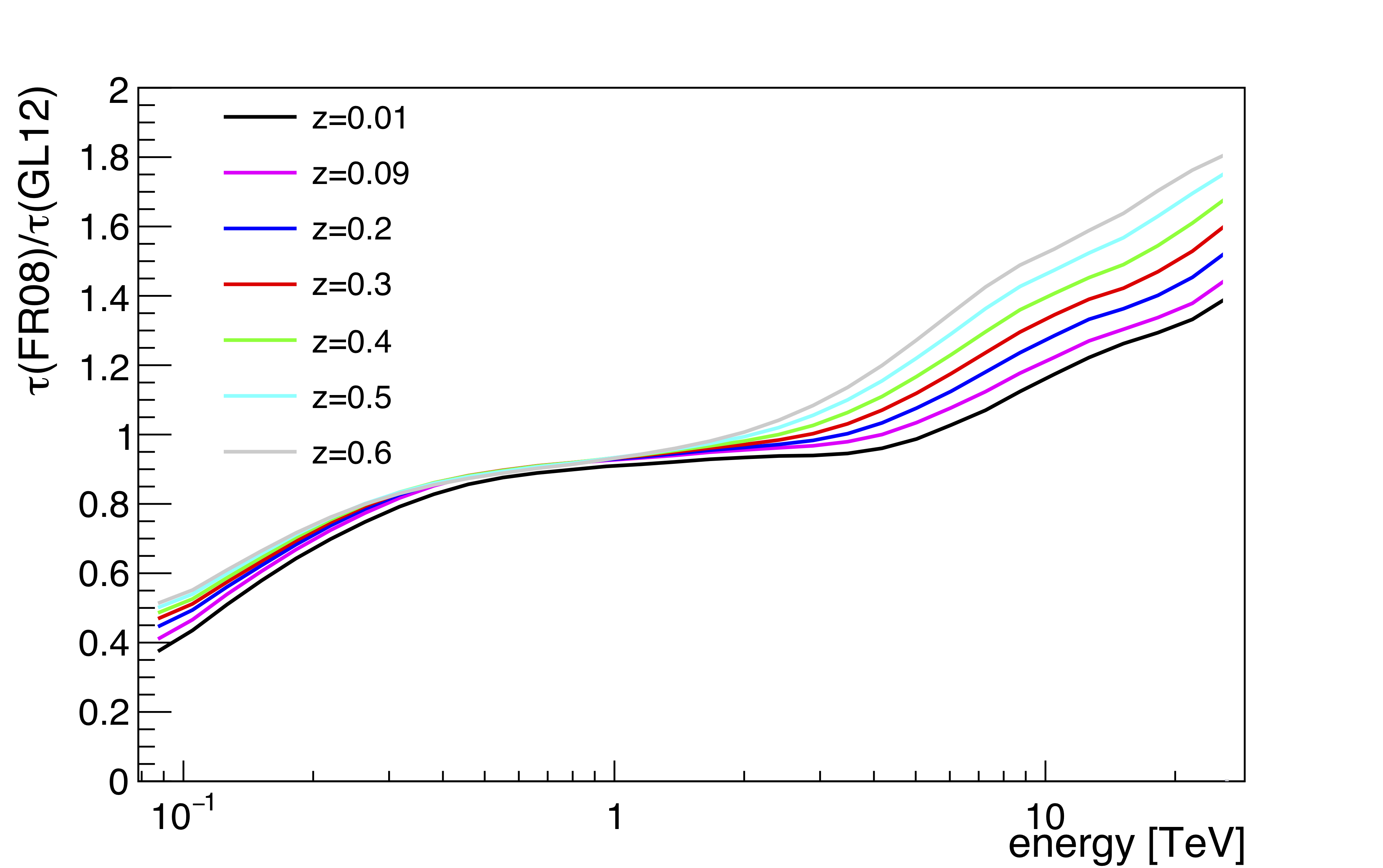
of blazar photon spectra. As photons from distant blazars travel to Earth, they interact with the EBL, resulting in pair production of electrons and positrons. This causes an energy- and distance-dependent attenuation of the photon flux arriving at Earth. With some assumptions about blazar intrinsic photon spectra and the evolution of the EBL density with distance, the observed spectra can be used to constrain the EBL spectral energy distribution (SED).

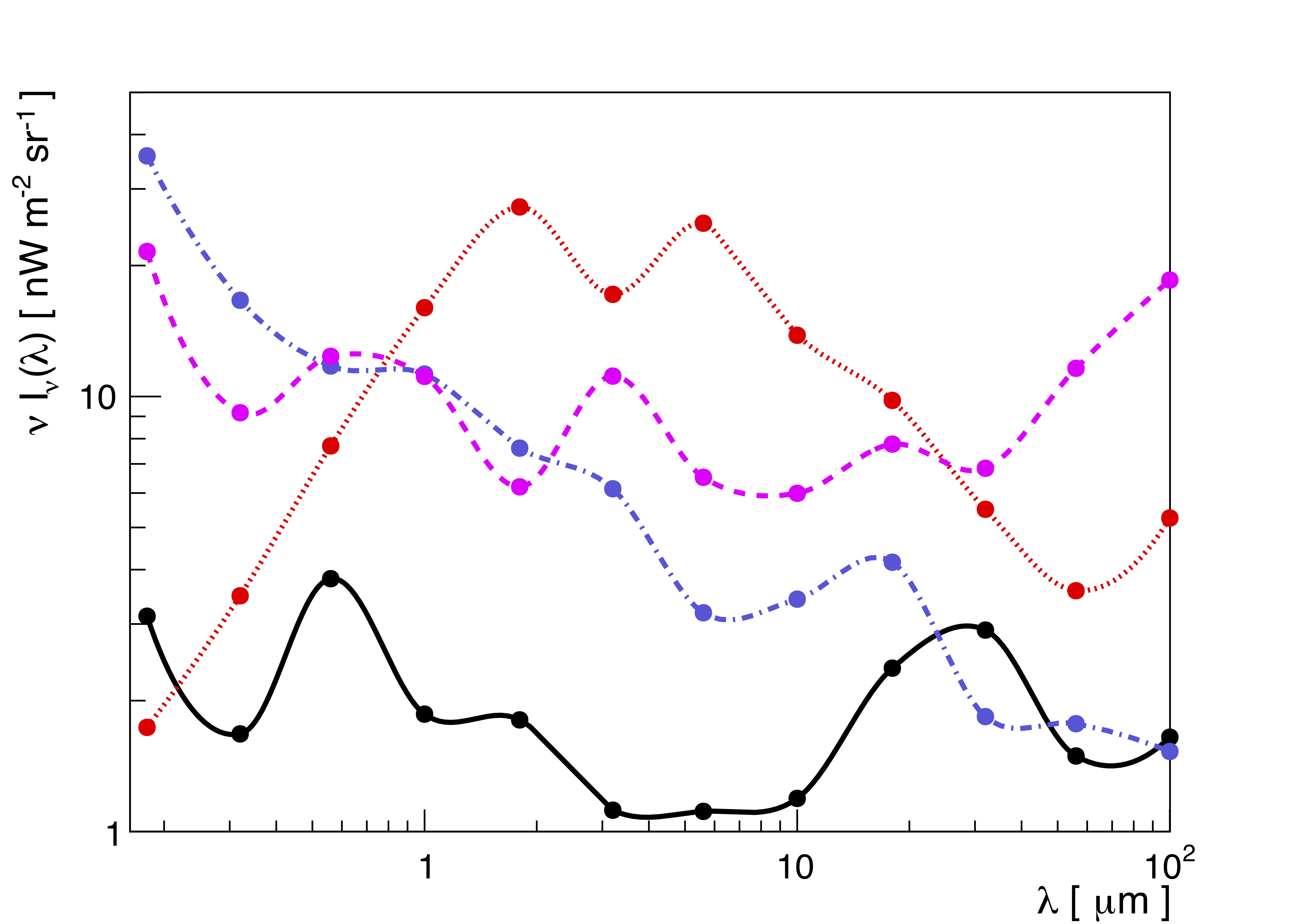
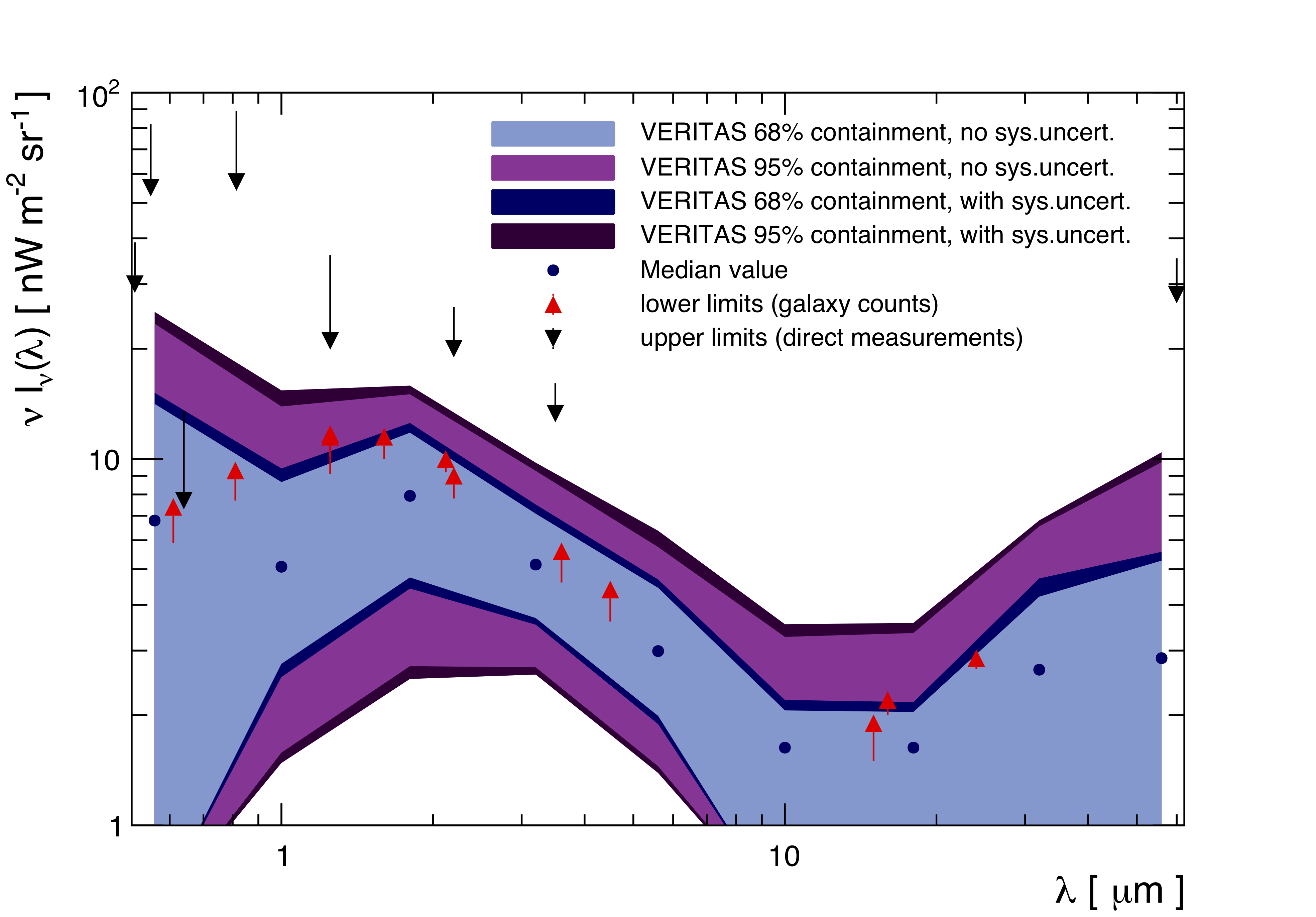
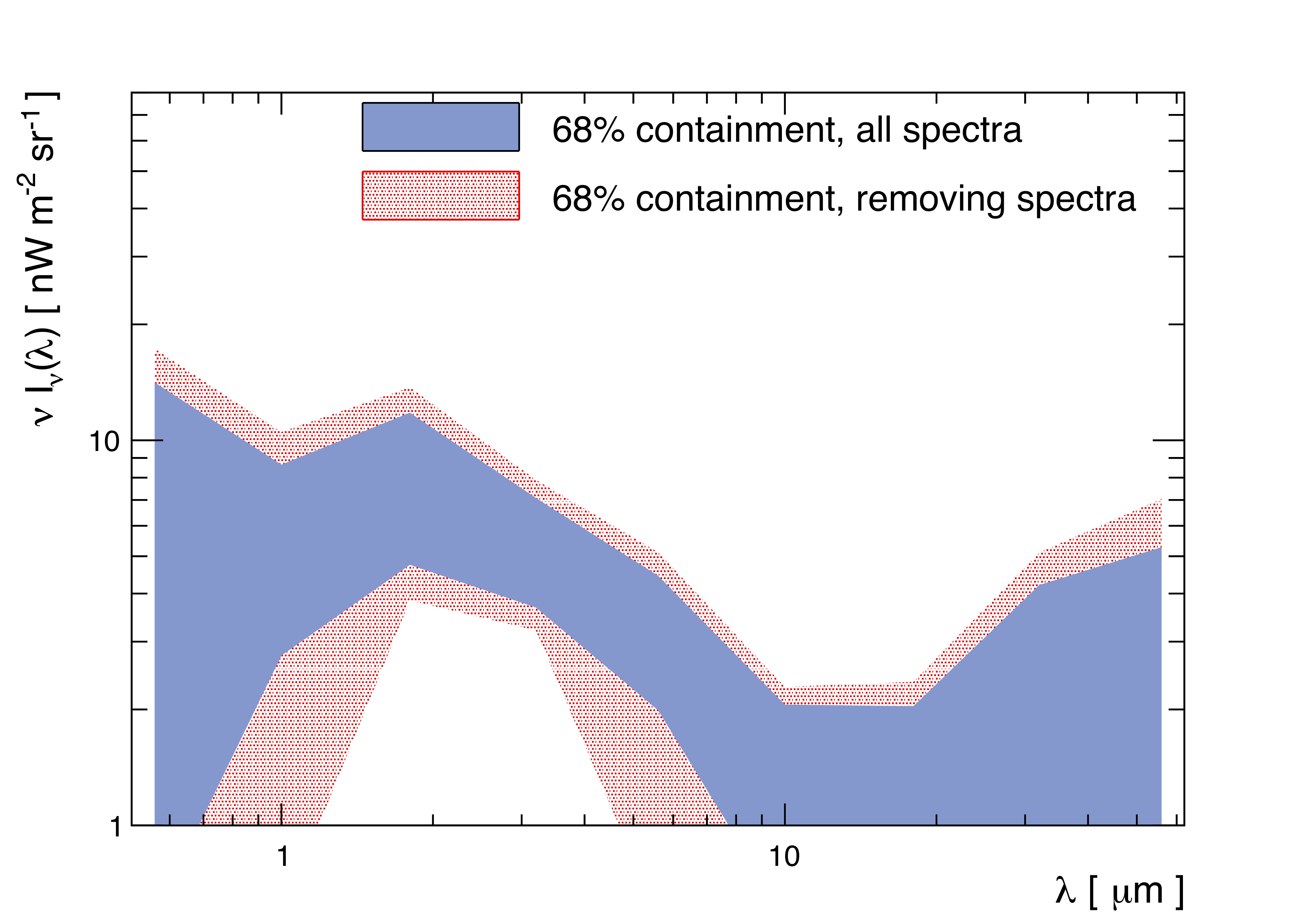
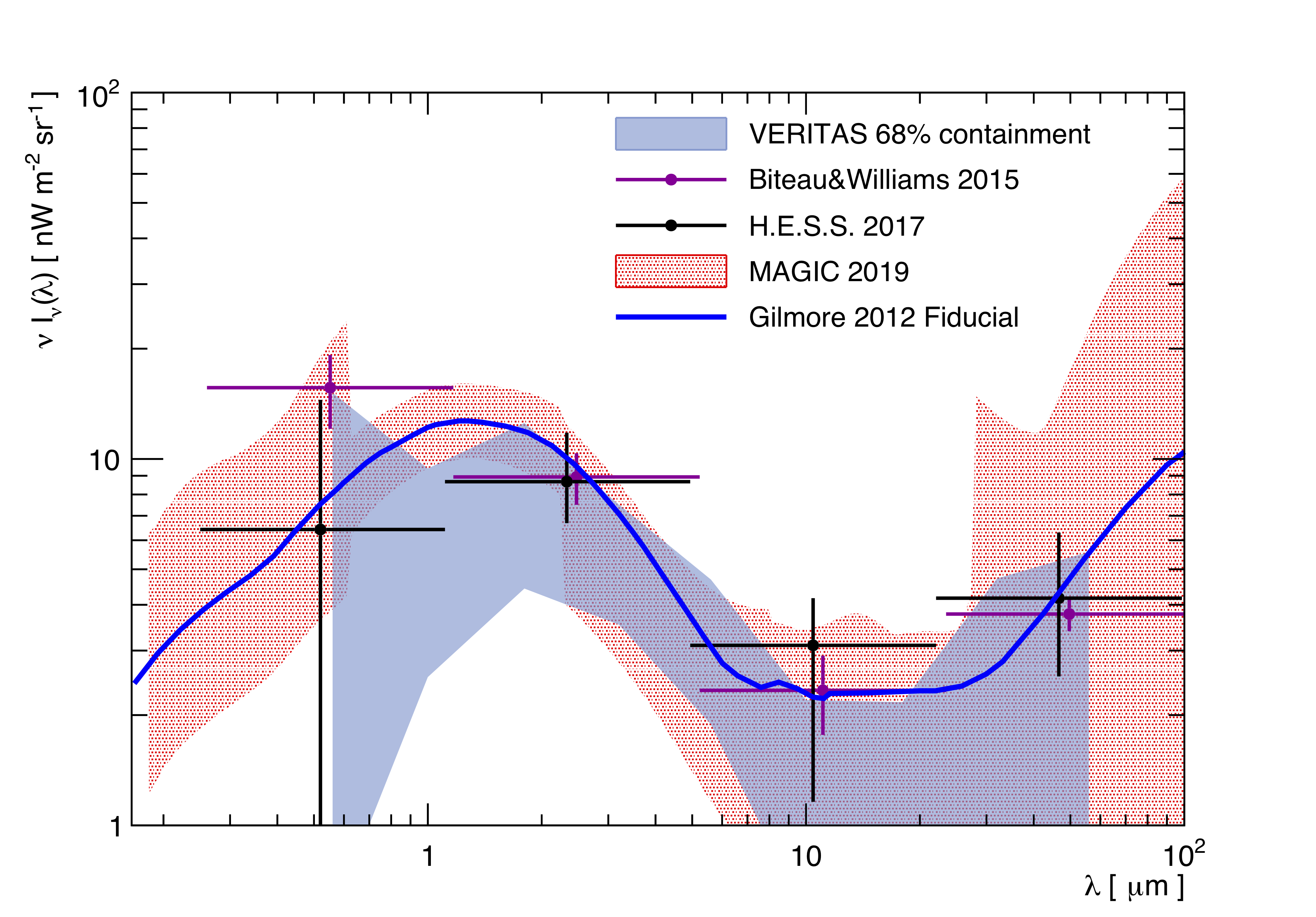
We present a measurement of the EBL SED in a wavelength range from 0.56 to 56 microns. The measurement is based on a spectral study of 14 blazars spanning 10 years of VERITAS observations. A set of minimal assumptions are made about the blazar intrinsic photon spectra, namely that they cannot have spectral upturns, and that there is a maximum hardness for the spectral index. The SED is in good agreement with lower limits on the EBL density, derived by summing the light from cataloged galaxies. Although the uncertainties are large, this measurement leaves a limited budget for additional components.

 

FITS files: N/A

Figures from paper (click to get full size image):

 

Figure 1:  Several examples of generic EBL shapes, de fined as EBL intensity as a function of λ EBL. The markers indicate grid points in λEBL at which a random number is drawn to describe the EBL intensity.
Figure 2: Example EBL intensity probability distributions. The shaded bands indicate the 68% containment bands. In the left panel, a two-sided containment band for ν I ν(λ ) can be extracted, whereas in the right panel only an upper limit can be set.
Figure 3: The ratio of τ(E) predicted by the models of Franceschini et al. (2008) (FR08) and Gilmore et al. (2012) (GL2012).
Figure 4: Measured 68% and 95% containment bands on the EBL intensity as a function of wavelength. The dark and light shaded regions illustrate the bands with and without systematic uncertainties, respectively. The fi lled circles mark the median values of the EBL intensity probability distributions. Upward-facing arrows show lower limits from galaxy counts, downward-facing arrows show upper limits from direct measurements.
Figure 5: Measured 68% containment bands on the EBL intensity as a function of EBL wavelength, taking the most conservative bands obtained after removing the sources individually, overplotted with the 68% containment band including all spectra (without systematic uncertainties).
Figure 6: Measured 68% containment on the EBL intensity as a function of wavelength, compared to the recent gamma-ray measurements of Biteau & Williams (2015), H.E.S.S. (Abdalla et al. 2017), and MAGIC (Acciari et al. 2019), and the model of Gilmore et al. (2012).